Si, comme moi, vous êtes nul en maths, mais que vous rêvez d'envoyer un mobile à un endroit précis de la Planète, ce petit tuto est fait pour vous.
Je vais vous expliquer comment déterminer très facilement un cap selon les données de Latitude et longitude de votre module GPS.
Le principe est celui des calculs simples sur les triangles-rectangles et sur les "pentes", principalement utilisés par les charpentiers-couvreurs et autres maçons.
2 raisons a ce choix:
- Je suis nul en maths mais je veux absolument maitriser et comprendre comment mon mobile calcule son cap.
-De base, et a moins d'intégrer de gourmandes librairies, l'Arduino ne dispose pas des fonctions mathématiques "arctan" ou autres, permettant de convertir des pourcents en degrés... Et la plupart des tutos que j'ai trouvé sont imbuvables.
Ce système utilise énormément d’opérations de comparaison, mais peu d'opérations de calcul, ce qui est un confort pour notre microcontrôleur.
Principe de calcul de la Pente:
En utilisant cette formule de couvreur, pour calculer le pourcentage de la pente d'un toit, il suffit de poser l'opération suivante:
pente (%) = 100 x hauteur / largeur
ou:
pente (%) = 100 x Plus petit côté du rectangle / plus grand côté du rectangle
Note: Dans ce principe de calcul de pente en pourcentage, le résultat de l’opération fait que la pente ne peut jamais représenter plus de 100% .
Ce "100%" représente une valeur de 45°. Donc, la pente ne peux jamais dépasser la valeur de 45°.
Nous allons voir comment on détermine le triangle-rectangle pour calculer la pente et comment s'affranchir facilement de la limitation des "45°".
Tout d'abord, il nous faut les coordonnées de départ et les coordonnées de destination.
Premier point important:
Prenez bien note que les "coordonnées de départ" deviendront les coordonnées de route, dès que votre mobile aura quitté le plancher des vaches.
Le mobile recalculera son cap a intervalles réguliers pour vérifier sa position actuelle donnée par son GPS embarqué.
Les coordonnées de destination sont normalement rentrées une fois pour toute avant le départ du mobile.
On peut cependant prévoir plusieurs "points de passage" sur la route, pour prendre des photos, etc...
Nous allons commencer par un exemple.
Imaginons un trajet de Tours à Orléans.
Sur Géoportail IGN ou Map, nous trouvons pour ces deux ville les coordonnées suivantes:
Départ : Tours= Lat: 47.3771,N Long: 0.7082,E
Arrivée : Orléans= Lat: 47.9027,N Long: 1.9057,E
Sans nous aider de cartes, nous allons de suite déduire de ces coordonnées plusieurs éléments simples qui seront importants pour la suite des calculs:
- La latitude d’Orléans est
plus élevée que celle de Tours, notre mobile devra se diriger plutôt vers le
Nord...
- La Longitude d’Orléans est
plus élevée que celle de Tours,notre mobile devra se diriger plutôt vers l
'Est.
Donc, le cap aura donc une tendance de cap de base "
Nord-Est".
- Les deux Latitudes ont
le même sens :
Nord, Nord.
- Les deux Longitudes ont
le même sens :
Est, Est.
( Si nous envoyions notre mobile à Cochabamba, en Bolivie,
Coordonnées : 17° 23′ 00″ sud, 66° 10′ 00″ ouest,
La destination du mobile se situerait alors dans l'hémisphère Sud ainsi que dans les coordonnées West du méridien de Greenwich...)
Nous verrons plus loin que cette notion de "Sens" influe sur le calcul des dimensions du triangle-rectangle.
Nous allons maintenant définir le cap vrai avec beaucoup plus de précision.
Si vous regardez une mappemonde, vous constaterez que les "tranches" des longitudes se resserrent de plus en plus aux pôles tandis que les "disques" des latitudes, eux, restent a égales distances entre eux...
la distance en Km d'1 degré de longitude dépend a quelle latitude il est calculé:
A l'équateur, par exemple, ou la latitude est à 0°, 1 degré de longitude représente 200, 335 Km...
A Dunkerque, nous somme déjà à 51° Nord de latitude et 1 degré de longitude ne représente plus que 69,740 Km.
A Perpignan, nous somme à 42° Nord de latitude et 1 degré de longitude représente 80,850 Km
Nous décidons donc que, pour la France, 1 degré de longitude correspond à 75,84 Km (75840 m).
En ce qui concerne la latitude, elle ne change pratiquement pas et nous prendrons donc une moyenne de 111,73 Km (111730 m) par degré.
Consultez le site:
http://www.francetopo.fr/
Il posséde une règle trés pratique pour mesurer des distances...
Pour matérialiser les dimensions de notre rectangle, il faut:
-Soustraire la plus grande valeur des Latitudes de la plus petite:
47.9027 - 47.3771 = 0,5256
-Multiplier la valeur trouvée par le nombre de mètres que représente 1° de latitude:
0,5256 (°) x 111730 m= 58725 m
-Soustraire la plus grande valeur des Longitudes de la plus petite:
1.9057 - 0.7082 = 1,1975
-Multiplier la valeur trouvée par le nombre de Kilomètres que représente 1° de longitude:
1,1975(°) x 75840 m = 90818 m
Note: Comme nous le verrons plus loin, ce calcul n'est valable que si le "sens" des coordonnées sont identiques...
Notre rectangle fait donc 58725 m sur 90818 m
Plus haut, nous avons déjà constaté que notre cap avait une tendance de base "
Nord-Est".
La valeur de la longitude (en degrés) étant
plus grande que la valeur de la latitude (notre rectangle est plutôt "horizontal", ou plat...), on en déduit qu'on est dans une tendance de cap "
Nord, Est, Est".
(Si la valeur de la longitude (en degrés) était
plus petite que la valeur de la latitude (notre rectangle serait alors plutôt "vertical", ou haut...), on en déduirait qu'on est dans une tendance de cap "
Nord, Nord, Est".
Nous verrons leur importance un peu plus bas...
Attention de ne pas confondre les degrés avec les Kilomètres!
- On définit les dimensions du triangle-rectangle avec des unités métriques ( mètres ou kilomètres)
-On définit les "tendances de cap" avec des degrés.
En reprenant donc les dimensions de notre rectangle qui fait 58725 m sur 90818 m, nous posons l'opération suivante:100 * 58725 / 90818 = 64,66 %
Rappel : Dans ce principe de calcul de pente en pourcentage, le résultat de l’opération fait que la pente ne peut jamais représenter plus de 100% et donc ne jamais présenter un nombre de degrés supérieur a 45°.
On trouve dans la table de conversion.
64,66% = ~ 33°.
Comme on est dans une tendance de cap "Nord, Est, Est", et comme on le verra plus loin, il nous faut retrancher cette valeur a 90°, ce qui donne:
90° - 33 = Cap = ~ 57°
________________________________________________________________________________
Pourquoi les "tendances de cap" sont t'elles importantes?
- Par ce qu'avec le principe de calcul de pente, nous avons vu qu'on ne pouvais pas mesurer des angles supérieurs a 45°.
Cela n'est pas un problème, car, comme nous l'avons vu plus haut, il suffit de vérifier la hauteur et la largeur (en degrés et non en Km) du rectangle pour en déduire la tendance de cap, puis, selon cette tendance, d'ajouter ou retrancher les degrés (multiples de 45) si nécessaire, afin de reconstituer le cap vrai.
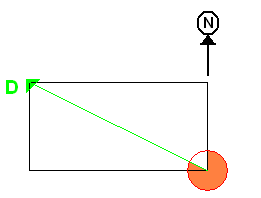
Des dessins valent mieux qu'un tas d’explications:
Le cercle orange représente un rapporteur complet (360°) dont le "0" est
toujours orienté vers le Nord.
La Latitude > Longitude && tendance N,N,E (le rectangle est vertical )=
Cap = Pente en degrés.
(comme une direction Paris-Laon, par exemple)
La
tendance "Nord,Nord,Est" est la seule tendance où nous n'avons pas a
ajouter ou retrancher de degrés complémentaires a la fin du calcul!
______________________________________________________________________
La Latitude < Longitude && tendance N,E,E (le rectangle est horizontal)=
Cap = 90 - Pente en degré.
(comme une direction Paris-Bruxelles, par exemple)
______________________________________________________________________
La Latitude > Longitude && tendance S,S,E (le rectangle est vertical )=
Cap = 180 - Pente en degré.
(comme une direction Paris-Lyon, par exemple)
______________________________________________________________________
La Latitude < Longitude && tendance S,E,E (le rectangle est horizontal)=
Cap = 90 + Pente en degré.
(comme une direction Paris-Monaco, par exemple)
______________________________________________________________________
La Latitude > Longitude && tendance S,S,W (le rectangle est vertical )=
Cap = 180 + Pente en degré.
(comme une direction Paris-Bayonne, par exemple)
______________________________________________________________________
La Latitude < Longitude && tendance S,W,W (le rectangle est horizontal)=
Cap = 270 - Pente en degré.
(comme une direction Paris-La Rochelle, par exemple)
______________________________________________________________________
La Latitude > Longitude && tendance N,N,W (le rectangle est vertical )=
Cap = 360 - Pente en degré.
(comme une direction Paris-Dieppe, par exemple)
______________________________________________________________________
La Latitude < Longitude && tendance N,W,W (le rectangle est horizontal)=
Cap = 270 +Pente en degré.
(comme une direction Paris-Caen, par exemple)
______________________________________________________________________
Donc, pour résumer:
tendance N,N,E : Cap = Pente en degrés.
tendance N,E,E : Cap = 90 - Pente en degré.
tendance S,S,E : Cap = 180 - Pente en degré.
tendance S,E,E : Cap = 90 + Pente en degré.
tendance S,S,W : Cap = 180 + Pente en degré.
tendance S,W,W : Cap = 270 - Pente en degré.
tendance N,N,W: Cap = 360 - Pente en degré.
tendance N,W,W: Cap = 270 +Pente en degré.
Essayez de trouver une petite carte de France ou du Monde avec les Latitudes & les Longitudes et entrainez-vous à dessiner les différents triangles-rectangles avec les 8 tendances possible, afin de vous familiariser avec le principe.
Fixez votre carte sur un mur et avec des punaises et de la ficelle, matérialisez les triangles-rectangles puis tirez les diagonales avec du fil de couleur différents...
Ci-dessous le tableau de conversion a entrer dans la mémoire de l'Arduino.
Il a été calculé avec des pas de 3°, de 0° a 45°,( ce qui représente 17 valeurs) ce qui est suffisant pour calculer un cap et ne pas surcharger la mémoire du module Arduino.
degrés pourcentage
0 0
3 5.241
6 10.51
9 15.838
12 21.256
15 26.795
18 32.492
21 38.386
24 44.523
27 50.953
30 57.735
33 64.941
36 72.654
39 80.978
42 90.04
45 100
On peut constater que plus les triangles-rectangles sont plats (en
hauteur ou en largeur), plus on s'approche des coordonnées de base :
Nord,Sud,Est,West.
Liens utiles pour vérifier les calculs de conversion de pourcents en degrés:
http://www.skitour.fr/divers/conversion-pourcentage-degre.php
Vous pourriez penser qu'une précision de 3° n'est pas "top", mais en fait, ce n'est pas du tout un problème. Le mobile recalcule son cap à intervalles régulier et plus il s'approche de sa destination, plus le cap est précis.
Si vous en avez le courage, tentez l’expérience en essayant de vous rendre a pied dans un endroit prés de chez vous, (environ 1 Km) muni juste d'un rapporteur et en vous donnant une marge d'erreur approximative de trois degrés. Vous recalculez votre position tous les dix mètres environ. Vous constaterez que vous arriverez facilement et parfaitement a destination.
Pourquoi le "Sens" a t'il une importance?
Comme nous l'avons vu plus haut, il est important de savoir si notre destination se trouve dans un autre hémisphère que celui de départ.
Notre GPS M6 MV2 nous indique
"N","S","E" W", et non pas des valeurs négatives, comme d'autres modèles le font.
Cela est important pour le calcul des dimensions de notre triangle-rectangle.
En effet, dans ce cas, par exemple, une des dimension de notre rectangle peut faire -5° (soit 5° Nord) sur 5°(soit 5° Sud).
Vous l’aurez compris; dans ce cas,
il faut additionner et non pas soustraire les degrés pour reconstituer les dimensions de notre rectangle, tant que notre GPS nous indique un sens différent de route et de destination...
Ha les maths et les nombres relatifs! (voyez plus de détails sur internet...)
Sinon, découpez un petit rectangle de quelques degrés que vous baladerez sur votre planisphère pour appréhender et comprendre le principe...
Sinon, cela ne change rien au reste du calcul.
Lien utile pour vérifier les calculs de cap:
https://www.sunearthtools.com/fr/tools/distance.php
J'ai testé cette théorie avec l'IDE Processing, qui s'apparente a l'IDE Arduino, afin de ne pas surcharger le microcontrôleur avec des tests répétitifs...
Dans une autre partie, nous allons mettre tous les calculs de façon assimilable par l'Arduino.